啥是I/Q Data
这篇文章主要介绍如何用 I/Q 数据来表示一个信号。非本专业的童鞋或者刚念大二大三的童鞋看了可能会非常疑惑,所以这篇文章我将用不同的角度来描述它。如果你觉得看不懂,那么继续往下看,后面可能会更容易理解——希望如此。
为什么要使用 I/Q 数据
如果让你用一串数据来表示一个信号,你会如何表示?最直观的方式是使用一串信号振幅的采样序列,如下图:
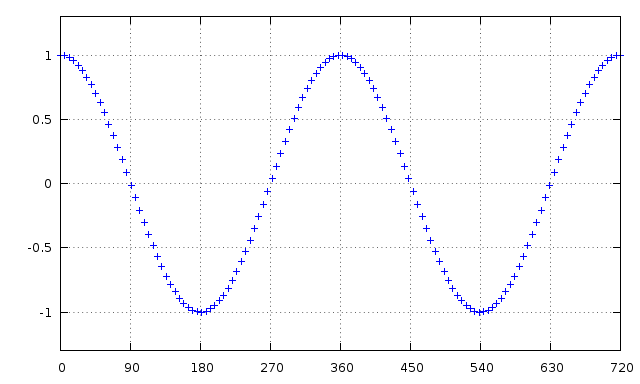
那为什么要多此一举使用 I/Q 数据来表示呢,采样序列的方式不够好吗?
事实上确实不够好,有下面一些问题:
- 首先,这样表示无法确定信号的频率。当然这样表示看起来非常简单,也非常直观,你可能会说,这样表示可以通过看信号的周期的方式来确定频率。当然这样做没错,但是问题在于,即使某个信号是从同一条曲线采样出来的花,你也无法确定这是一个正频率还是一个负频率,例如 : cos(x) = cos(-x) 。在你对信号处理的时候,这将成为一个麻烦。将两个信号相乘时,它将导致乘法的结果可能有好几个:f1 ⊗ f2 等于 f1 + f2 也等于 f1 - f2。
- 其次,这样也很难确定信号的功率(峰值振幅,包络)。基本上你只能在 0°, 180°, 360° 的时候看到峰值振幅,而且你也不能确定后续的信号的功率是否也是一致。而且你也无法确定你就在峰值那一点上采到了样,真的很难确定。
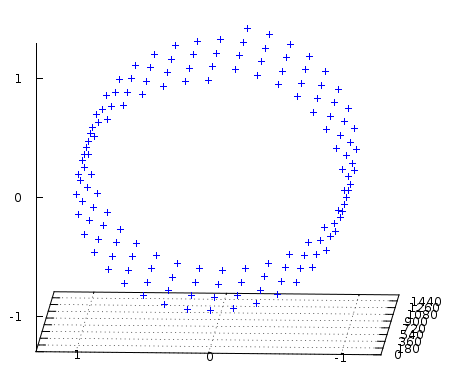
I/Q 数据解决了这些问题。它不是只在时间维度上对信号一维采样,而是把它在三维空间中看成一个螺丝(螺旋,螺旋弹簧)。
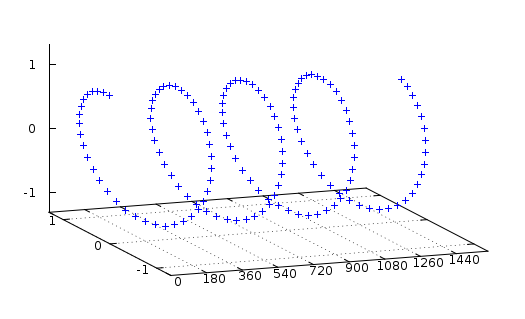
如果你从正面看这条三维曲线,你将会得到和上面一样的一幅图片。也就是说,采样序列也就是这个螺旋在 2D 上的投影。而这就是 I/Q 数据的 "I" 部分。
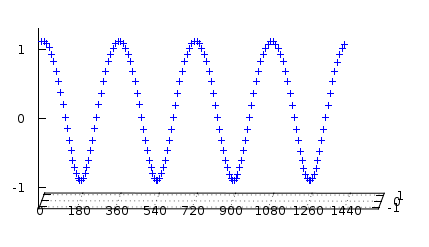
如果你从上方看这条三维曲线,看起来和从侧面看十分相似,但是注意到,它是从 0 而不是从 90° 相位开始的。这是 I/Q 数据的 "Q" 部分。
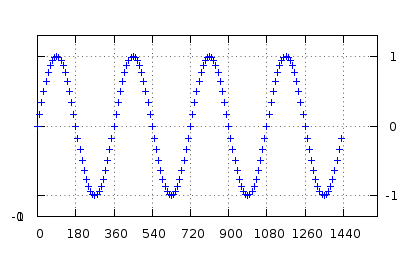
如果你沿着时间轴从侧面看这条曲线,你将可以看到,这条曲线是逆时针螺旋的。这意味着我们知道这个信号的频率为正。而当曲线顺时针螺旋时,我们也可以得出信号频率为负的结论。也就是说在 I 信号一样、Q 信号不一样的时候,可能能表达相反的频率。
你也可以看到,即使 I 变小、Q 变大,或者 Q 变小、I 变大,这条螺旋的半径在每个点上也都是一致的。而这个半径也就是信号的幅值。
I 轴和 Q 轴是互相垂直的,那么幅值也就等于 (I²+Q²)1/2 ,因此,在每个采样点都能看到信号的幅值。
I/Q 数据究竟是什么?
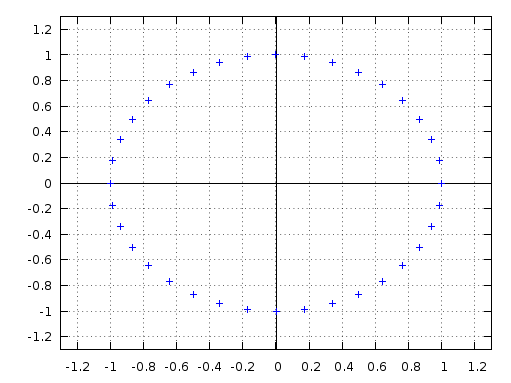
正如你所理解的这样,I/Q数据采样就是沿着这个螺旋的时间轴方向对信号的采样坐标。你可能会提出疑问,你的信号如果不是一个完美的cosine函数该怎样。但是你的信号的每个采样点都能像这样表示:
信号的每一个点都能用这个函数表示:A⋅cos(ϕ)
你可以给定幅值 A 和 角度 ϕ 为任意值(只要信号是连续的)。 而A⋅cos(ϕ) 就是 I/Q信号中的I分量,即你的实信号。请注意,这只描述了你的信号中的一个点,或者说,一个采样值。在下一次采样时将会生成新的I/Q值,即另一个幅度和相位角,而这,反映了信号的调制。
I/Q 数据的一个例子
现在,让我们用一个I/Q数据的例子来作为例子来看看是如何表示的。这也叫做相位矢量(phase vector),或者相量(phasor)。
I = 0.69
Q = 0.40
画出复平面坐标图:
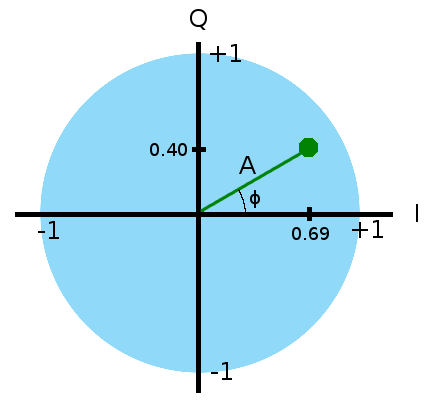
让我们来看看上面这幅图告诉了我们什么:
- 瞬时幅值由信号的实部I给出,即 0.69
- 毕达哥拉斯定理告诉我们这整个信号的幅值是:(0.69²+0.40²)1/2 = 0.8
- 三角函数告诉我们,目前相位角是在cosine函数的+30°
等等,这个cosine函数是什么?
当然,I/Q事实上假定了你的实信号(I)能表达为这个函数 I = A⋅cos(ϕ)
既然你能够自由选择A和ϕ,那么只要信号连续的话,上面表达式就绝对成立。
所以,使用IQ数据时,我们不仅仅能得到信号的瞬时值,而且可以得到一个生成函数。综上所述,我们可以得到:
实信号 I = 0.8⋅cos(30°)
换句话说,I/Q数据是cosine函数的一种表达形式。
而I/Q数据是我们上面使用的极坐标符号的矩形表示。这两者之间能互相转换,且不同的表达方式有不同的计算方式。选择矩形表示的I/Q数据是因为用硬件实现起来非常简单。
I/Q数据包括了I和Q两个独立的变量,它是一个长度为2的向量,或者说是一个复数I+Qi(当然,I是实部)。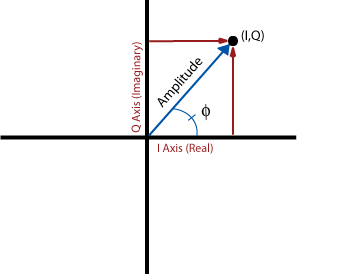
需要注意的是,上面所说的振幅是整个波的峰值振幅,而非瞬时振幅。
- I是这个信号的瞬时振幅(即真正的信号)
- Q是信号相位偏移的瞬时幅值-90°
对于一个简单的函数,如正弦,相移代表着信号早于某一时刻产生,但是对于一个由不同分量的正弦函数叠加的信号,Q反映的是单个分量的90°位移,而不是复合信号。要将一个真正的信号转换成I/Q数据信号,需要进行傅立叶变换。
标签: 无标签