对一道算法题的思考
Ch.1 前记
某日邹欣老师在群里出了一道题目。
题目如下:一个文本文件中有N 个不同的英语单词, 我们能否写一个程序,快速找出最长的能首尾相连的英语单词链,每个单词最多只能用一次。
例如, 文件里有:
Apple
Zoo
Elephant
Under
Fox
Dog
Leaf
Tree
最长的相连英语单词串为: apple - elephant – tree, 输出到文件里面,是这样的:
Apple
Elephant
Tree
要求程序 (WordList.exe)能处理命令行参数,知道什么是输入文件, 输出文件应该放在哪里。 这样,当助教拿到学生的源程序后,就能编译,并运行一系列的测试。
shell> Wordlist.exe /i input1.txt /o output1.txt
shell> Wordlist.exe /i input2.txt /o output2.txt
Ch.2 思路
乍看之下这道题目不是那么简单,但是仔细思考一下题目有的几个条件:第一,不区分大小写。第二,每个单词只能用一次,就不难发现,其实这道题是等效于求有向图的最小路径这类问题的,因为每个单词的首位字母实际上就是表示图的节点,单词的长度则表示节点之间的权重。
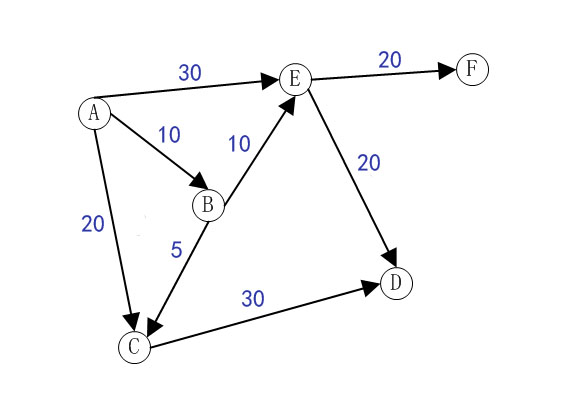
而提到有向图的最长/最短路径问题,就不得不说一下 NP、P、NPC、NP-hard的关系了。
P:多项式(polynomial),指能在多项式时间内解决的问题。NP:非确定性多项式(non-deterministic polynomial),指不能在多项式时间内解决的问题,但是能在多项式时间内验证问题。NPC:NP完全问题(NP complete),所有NP问题在多项式时间内都能约化(Reducibility)到它的NP问题,即解决了此NPC问题,所有NP问题也都得到解决。NP-Hard:NP难问题(NP hard)所有NP问题在多项式时间内都能约化(Reducibility)到它的问题(不一定是NP问题)。
著名的旅行商问题就是一个典型的NP问题,因为你可以很容易就说明每条路径的花费,但是无法证明这条路径是最优路径。但是我们这道题放宽了条件,首先节点的数量是有最大值26的(字母数量),其次,每两个节点之间的路径是可能有多条的且每条路径只能走一遍的(例如 ant 和 absent 这两个单词)。那么这道题还属于NP-Hard吗?
节点的数量是有限的,那么我们就可以通过遍历节点的方式来搜索最大的路径。这样做的缺点显而易见:计算量过大,而且和单词数量规模呈阶乘级别的时间复杂度,但是优点是能保存遍历的状态,下一次遍历之前能知道哪条路径是已经被用过的。
Ch.3 解法
最终还是没有想出来一个好的办法,只好用DFS遍历算法做了一遍,复杂度大概是O(n!),代码如下:
#include <iostream>
#include <vector>
#include <string>
#include <algorithm>
using namespace std;
#define _MAX_CELL 26
//DFS递归查询
pair<int, vector<int>> DFS(int index, vector<int> route[_MAX_CELL][_MAX_CELL])
{
unsigned int length = 0;
vector<int> rox;
pair<int, vector<int>> rtn;
rtn.second.push_back(index);
//寻找下一跳
for (int i = 0; i < _MAX_CELL; i++)
{
if (route[index][i].size() > 0)
{
sort(route[index][i].begin(), route[index][i].end());
int l = route[index][i].back();
route[index][i].pop_back();
//进入下一深度之前需要把这条路径暂时删除,因为每个单词只能用一次
pair<int, vector<int>> tx = DFS(i, route);
unsigned int tmp = l + tx.first;
route[index][i].push_back(l);
if (length < tmp)
{
length = tmp;
rox = tx.second;
}
}
}
rtn.first = length;
rtn.second.insert(rtn.second.end(), rox.begin(), rox.end());
return rtn;
}
void maxLength(vector<string> text)
{
vector<int> route[_MAX_CELL][_MAX_CELL];
vector<int> path[_MAX_CELL][_MAX_CELL];
int head[_MAX_CELL] = {0};
//构建邻接图
for (auto iter : text)
{
route[iter.front() - 'a'][iter.back() - 'a'].push_back(iter.size());
head[iter.front() - 'a'] = 1;
}
//DFS遍历所有头节点
pair<int, vector<int>> result = { 0, vector<int>{} };
for (int k = 0; k < _MAX_CELL; k++)
if (head[k] == 1)
{
pair<int, vector<int>> rt = DFS(k, route);
if (rt.first > result.first)
{
result = rt;
}
}
//打印
for (int i = 0; i < result.second.size()-1; i++)
for (auto iter = text.begin(); iter!= text.end(); iter++)
if ((*iter).front() == ('a' + result.second[i]) && (*iter).back() == ('a' + result.second[i + 1]))
{
cout << (*iter) << endl;
text.erase(iter);
break;
}
return;
}
int main(int argc, char * argv[])
{
//假设前级已经做了不合法数据验证
maxLength(vector<string>{
"apple",
"elephant",
"zoo",
"under",
"fox",
"dog",
"leaf",
"tree",
"text",
"text"
});
maxLength(vector<string>{
"apple",
"blephant",
"clephand",
"flephant"
});
return 0;
}
标签: 无标签